Simple Geospatial Methods
Simple geospatial methods estimate values at unsampled points with no statistical error model. They work best with larger data sets. No statistical assumptions are required, so they can be a quick, simple approach to modeling spatial trends. These methods, however, do not quantify prediction uncertainty. This section presents typical uses for simple geospatial methods, such as inverse distance weighting, Voronoi diagrams/Thiessen polygons, and natural neighbor interpolation. The assumptions, strengths, and weaknesses of each method are described, as well as guidance on using the method results.
Inverse Distance Weighting
Inverse distance weighting (IDW) interpolation applies multiplier values to the data points during interpolation so that the influence of one data point relative to another decreases with distance (d), using the weighting function w(d) = 1/dp, where the exponent “p” (or sometimes called weighting power) is usually user-specified. Higher exponent values make points far from a grid node have less effect on the interpolation at that grid node. As the exponent increases, there is less averaging, and the grid node value approaches the value of the nearest data point. As the exponent decreases, there is more averaging, and the weights are more evenly distributed among the surrounding data points (Golden Software 2002). This method is usually available in computer interpolation programs because it is fast, simple, and can accommodate very large data sets.
IDW normally behaves as an exact interpolator, with predicted values exactly coinciding to data values at measurement locations. Because there is no theoretical basis for selecting parameters, the power and search neighborhood terms should be specified based on minimizing cross-validation error. One characteristic of IDW interpolation is the generation of contour maps with bull’s-eye patterns around data points. Some software programs enable smoothing of contours, but this practice may not eliminate the bull’s-eye effect.
Typical Applications
Using this Method
Assumptions
Strengths and Weaknesses
Understanding the Results
Further Information
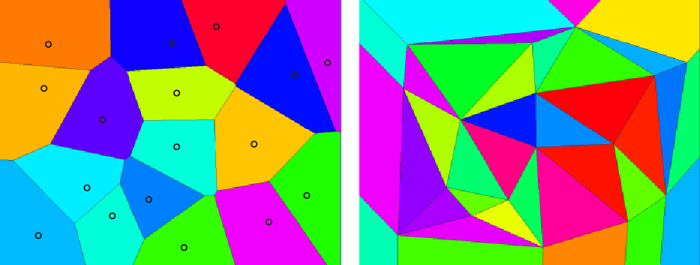
Thiessen Polygons, Delaunay Triangulation Diagrams and Voronoi Diagrams
Two closely related methods of characterizing spatial distribution and influence of sample points are Thiessen polygons and Delaunay triangulations. In each of these methods, the sampling area is divided into regions containing one sampling point. The regions then can be weighted according to the size of the area relative to the total area. For example, concentrations at unsampled points are estimated using a weighted average of the concentrations of adjacent points using the polygon areas for the weights.
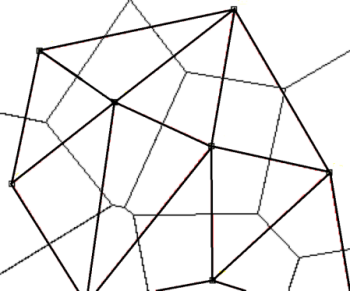
Delaunay Triangulation for Sampling Optimization
Delaunay triangulation may be used to determine the natural neighbors of a given sampling location. Areas with large differences in contaminant concentration between natural neighbors may then be targeted for additional sampling locations, while areas with small differences may require fewer sampling locations. Thiessen polygons (or Voronoi cells) may also be used to “weight” concentrations by the surface area enclosed in each. For example, each concentration can be assigned a weight equal to the ratio of the polygon area to the area of the site (or exposure unit in the case of a risk assessment). The weight then can be incorporated into subsequent statistical analyses to assign more impact to those concentrations representing larger surface areas.
Natural Neighbor Interpolation
Natural neighbor interpolation is a smoothing technique that allows for surrounding sample information to contribute to the estimation of values at unsampled points. The natural neighbor method is based on Thiessen polygons (or Voronoi cells) constructed from the set of sampling locations. For any point, its natural neighbors are the locations associated with the adjacent Thiessen polygons (ESRI 2012). The values of the unsampled points are estimated using a weighted average of the values of their natural neighbors using associated polygon areas for the weights. Figure 58 illustrates the Voronoi diagrams and Figure 59 illustrates Delaunay triangles with Voronoi cells; see also the relationship between Voronoi diagrams and Delaunay triangles.
Typical Applications
Using This Method
Assumptions
Strengths and Weaknesses
Understanding the Results
Further Information