Evaluate Geospatial Method Accuracy
Before using the predictions or prediction uncertainty estimates, the overall accuracy of the interpolation method or model must be assessed. The interpolated values should be checked to make sure they are consistent with the CSM and other source of information. In addition, the method should be evaluated using formal statistical methods for assessing model fit. The primary model assessment methods are cross-validation and validation.
▼Read more
Cross-Validation
Validation
Different sets of cross-validation and validation statistics are available for performing model diagnostics depending on the complexity of the model used. This method is further described in the sections below.
Determine Errors in Simple Methods
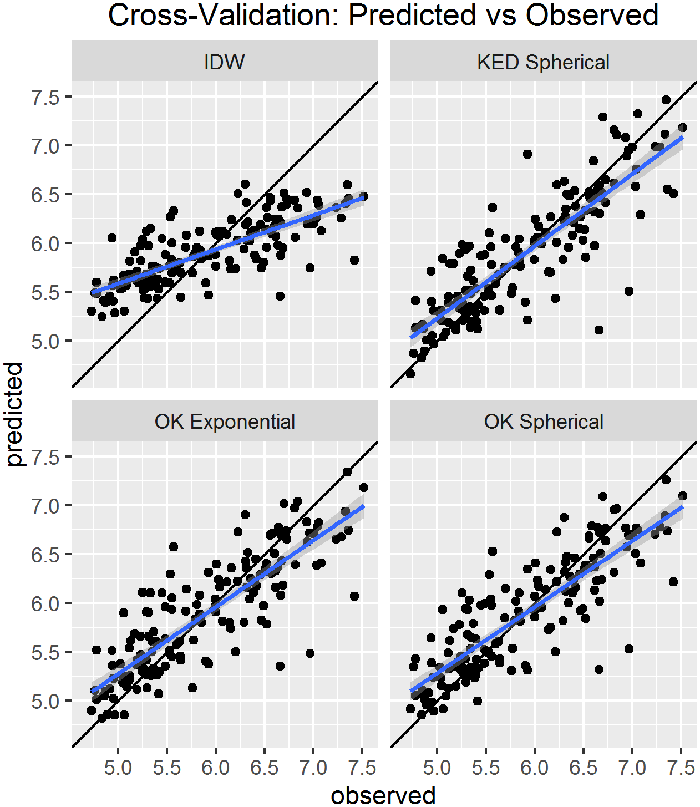
For simple geospatial models (for example, IDW), after computing the cross-validation or validation errors, the mean error (same units as the data, measuring the prediction bias) and the root-mean-square error (RMSE, measuring prediction accuracy) can be calculated. Simple methods do not estimate prediction uncertainty across sample locations; however, cross-validation may be used to estimate variation at individual sample locations.
Determine Errors in More Complex and Advanced Methods
In addition to predictions at unsampled locations, more complex (regression) and advanced (geostatistical) methods also provide the prediction standard errors that provide an estimate of uncertainty at each prediction location. Three additional metrics of method accuracy can be calculated: mean standardized error (dimensionless), average standard error (analogous to root mean square error), and root-mean-square standardized error (measuring the assessment of prediction variability). Beyond assessing the overall ability of the model to make good predictions, this additional set of statistics allows assessment of how accurately the model reflects the variability of the data. The mean error and RMSE are still useful metrics for advanced methods and should be calculated and presented as with simple methods.
Examples