Characteristics of Interpolation Methods
This section describes the characteristics of interpolation methods in general. The Methods section includes information about the individual methods. The Geospatial Work Flow section provides support in selecting methods for different sites and data sets.
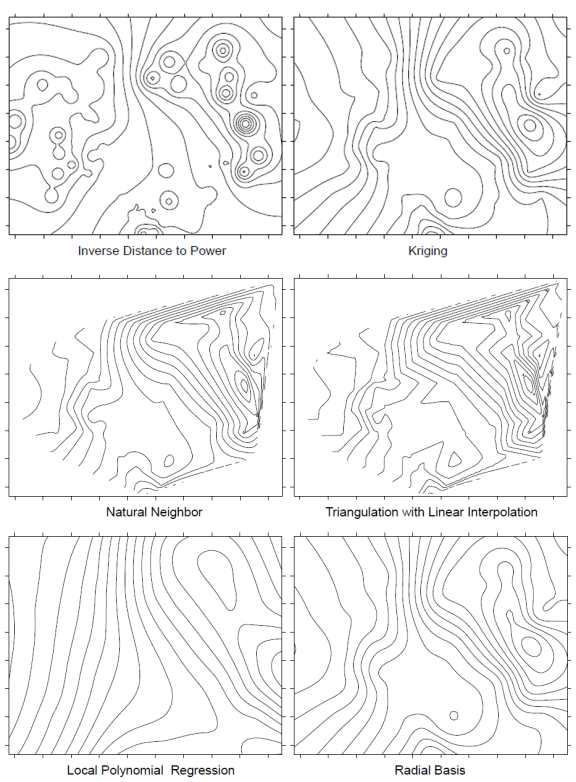
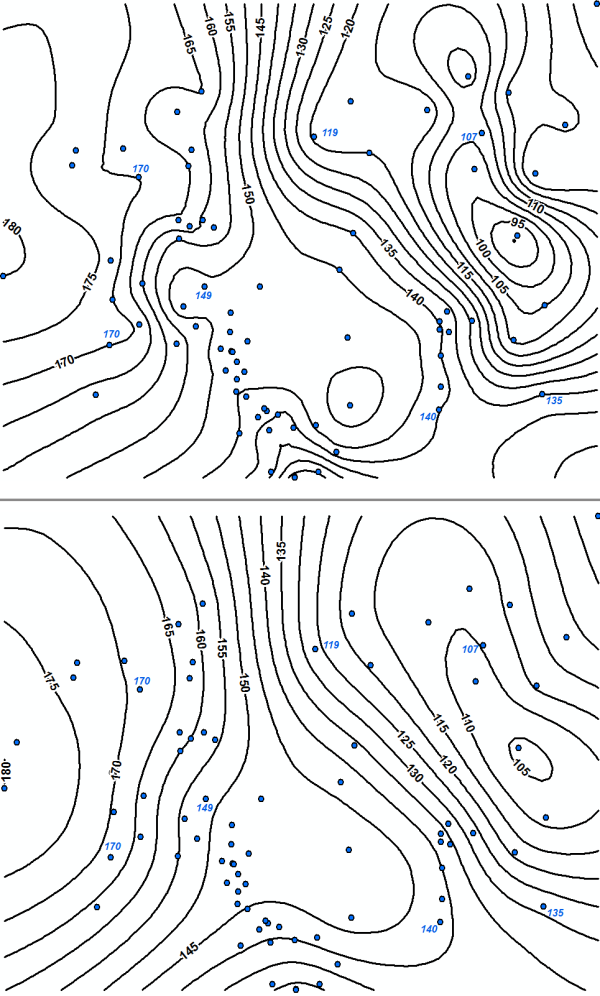
Different interpolation methods can result in different contour maps. Long range trend is common in environmental data sets and for some interpolation methods, the long range trend must be removed by detrending, described here, in order to obtain the best quality interpolation. Anisotropy occurs when the spatial correlation is different along different coordinate axes in the space and can also affect interpolation. Some interpolation methods take into account uncertainty in the measured data set. These methods, called inexact methods, may yield a contour map where a contour line may pass through a sampling point where the measured value is a little different from the value of that variable on the contour line.
The extent to which interpolation methods use the spatial or temporal correlation of the data to account for uncertainty is only one aspect of the interpolation process. Additional characteristics of the overall interpolation process discussed in this section include:
- long-range trend, anisotropy, and search neighborhood
- exact versus inexact interpolation
- interpolation boundary conditions
- interpolation gridding
Long-Range Trend, Anisotropy, and Search Neighborhood
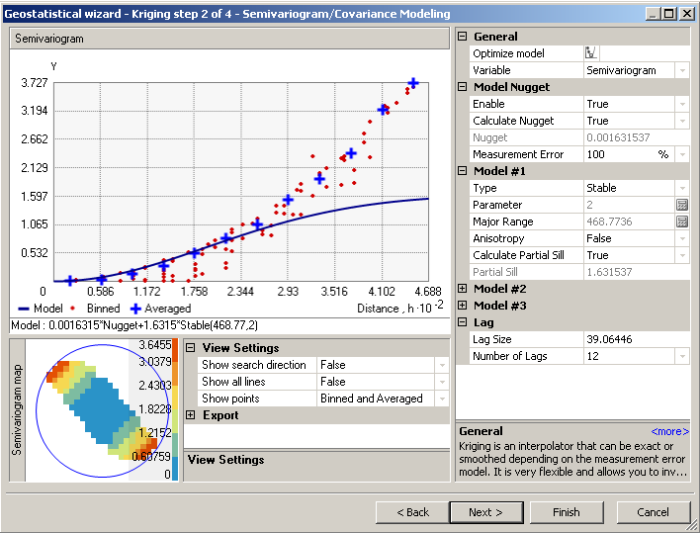
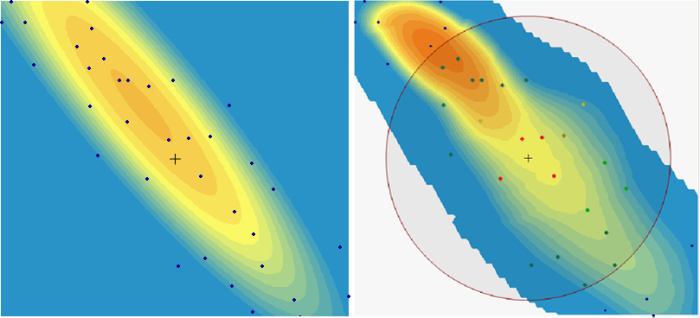
Environmental data commonly exhibit a long-range trend, which is typically expressed as a smooth, predictable change in values operating at a regional scale (Webster and Oliver 2001). Long-range trend is systematic and deterministic and is inherently variable, which affects kriging assumptions. Long-range trend should not be confused with geometric anisotropy, which is the directional dependence of spatial correlation. The search neighborhood defines the area over which data points are considered when interpolating a value at a new location.
Long-range trend▼Read more
Geometric Anisotropy ▼Read more
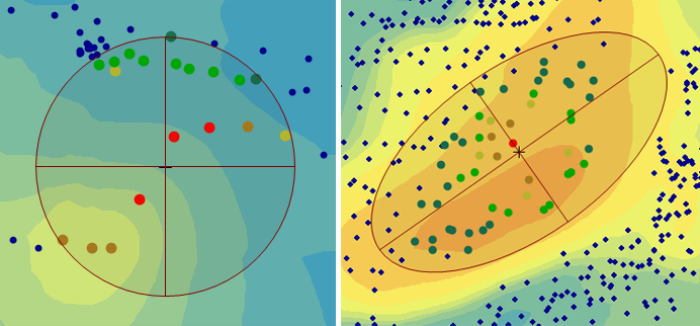
Search Neighborhood ▼Read more
Exact versus Inexact Interpolation
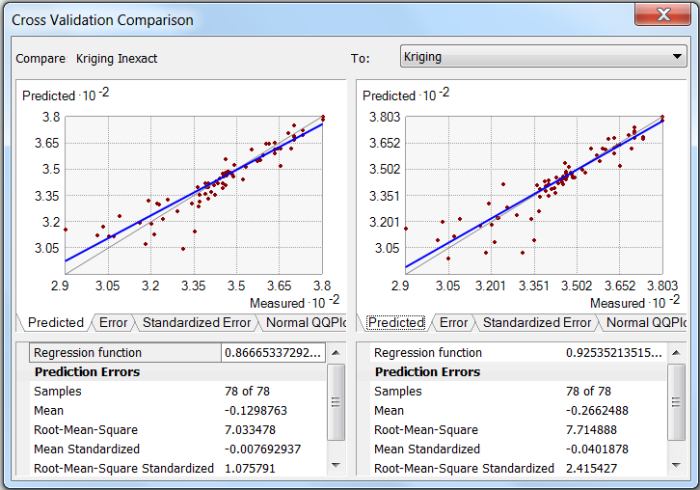
Interpolation methods can either be exact or inexact interpolators. An exact interpolator produces values exactly equal to observed values at all measurement locations. In other words, an interpolated contour line with a value of 10 would exactly pass through all measurement points with value of 10. An inexact interpolator accounts for uncertainty in the data by allowing the model to predict values at sampling locations that are different from the exact measurements. In this case, a contour line with a value of 9 may pass through a measurement point with a value of 10. Inexact interpolators are often referred to as smoothing interpolators because they produce smoother surfaces with fewer discontinuities that better reflect the spatial correlation of the broader data set (Golden Software 2002). Conversely, exact interpolators are forced to honor each individual data point regardless of uncertainty or measurement error, often resulting in jagged contour lines or surfaces with bull’s-eyes.
Interpolation Boundary Conditions (Breaklines, Barriers)
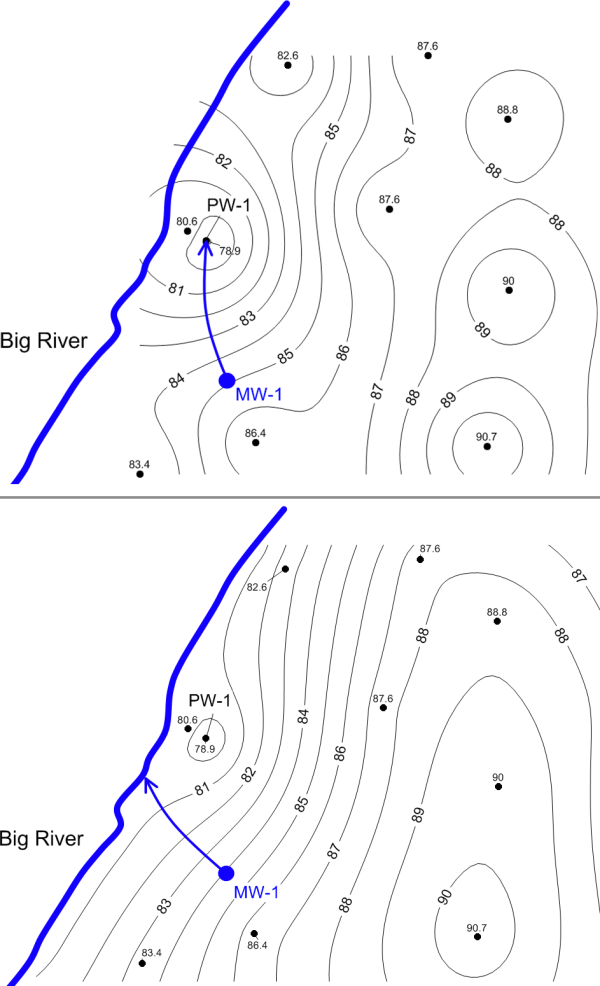
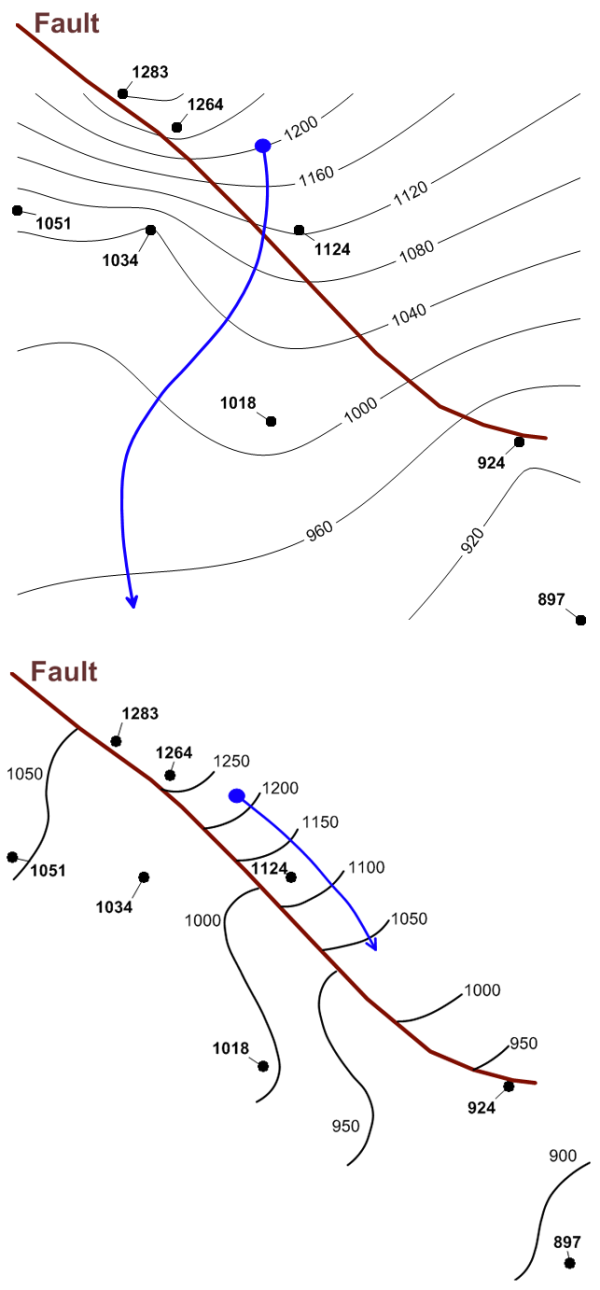
Spatial data at remediation sites are subject to boundary conditions that influence data orientation and correlation. The most common example is the influence of recharge and discharge boundaries on the groundwater potentiometric surface, which often results in long-range trend. Recharge boundaries may include injection wells, recharge basins, or losing streams, while discharge boundaries may include pumping wells, trenches and gaining streams. Another common boundary condition is a groundwater barrier, or no flow boundary. This barrier may include a bedrock contact, fault, or an engineered barrier such as a slurry wall or sheet pile. Boundary conditions can also produce other problems with the data set. These problems include edge effects, in which patterns of interaction or interdependency across the borders of the bounded region are ignored or distorted, and shape effects, in which the shape imposed on the bounded area affects the perceived interactions between phenomena (ESRI 2015a).
Interpolation Gridding
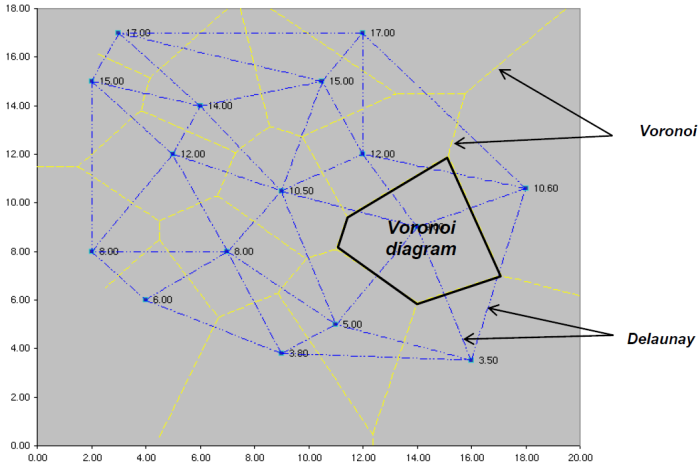
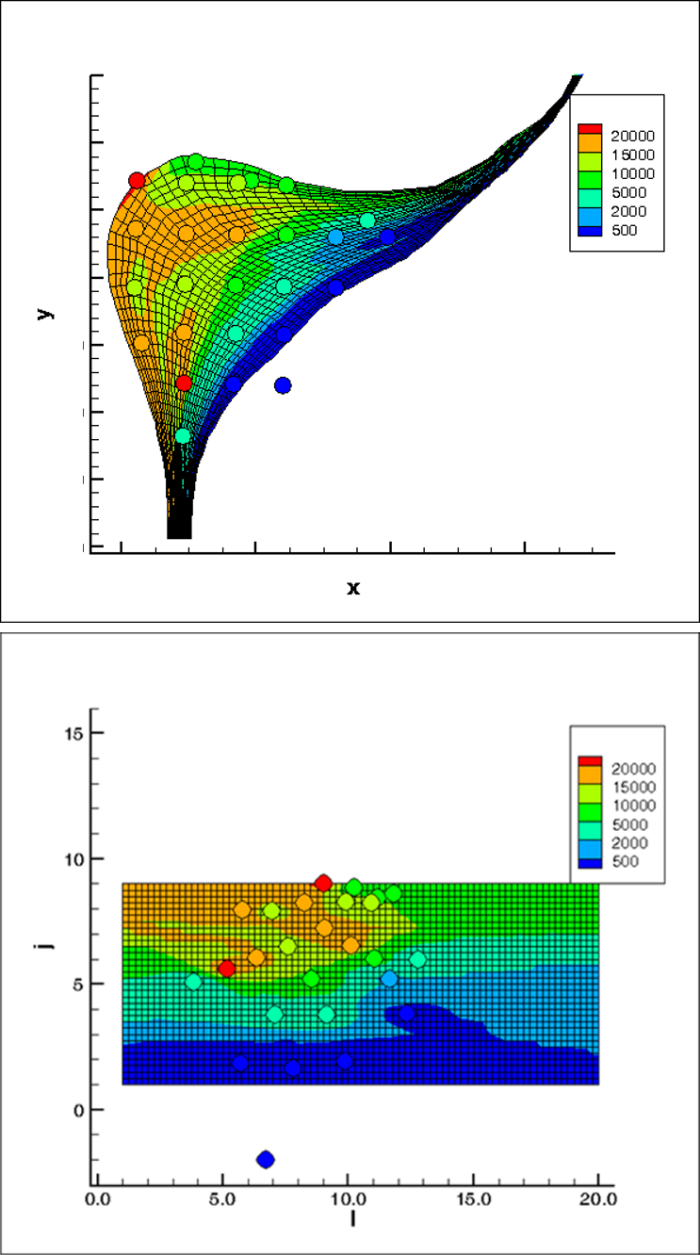
Regardless of the method used, the process of spatial interpolation with a computer program involves converting discrete point data (for example, monitoring well water level elevations or contaminant concentrations) to a continuous grid of predictions with at least one value associated with each grid cell. For example, a set of measured contaminant concentrations at specific well locations would be converted to a set of predicted contaminant concentrations at points across the grid. Such data on grids are termed raster data, and also may be referred to as surfaces. Grids produced by interpolation programs are typically square, but they may also be rectangular, curvilinear, or an unstructured finite element mesh. Delaunay triangulation is an example of a common unstructured grid used to generate a network of triangular shapes that are incrementally augmented through insertion of interpolated values into designated empty mesh cells. Several variations on the Delaunay algorithm exist and most are available in commercial modeling software through methods such as natural neighbor interpolation.
Delaunay triangles, Voronoi diagrams, Thiessen polygons
Grid spacing